MathsClass

I think that each student using a netbook/laptop in your class presents some slightly different issues in Maths.

So far, at least, most of the activities that I’ve had students working with on their laptops have been interactive widgets. (We’ve been doing algebraic techniques, index notation and solving equations since Year 9 got their laptops). For instance, here’s some of the activities we’ve used for equations:

• Solve 1-step equations – Battleship
• Equations Practice
  Solve equations by doing the same thing to both sides. Levels 1 and 2 have 1-step equations, level 3 has 2-step equations and level 4 has unknowns on both sides.
• Algebra Balance Scales
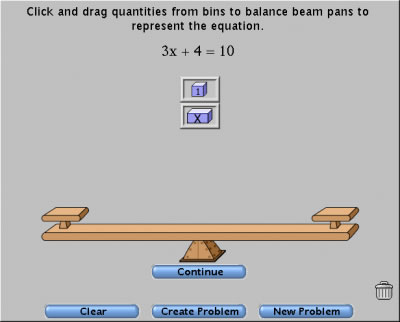
  Solve simple linear equations using a balance beam representation. 2-step equations.

Keep up with other activities like these as I categorise them in the Maths Links section. Better still, submit your own link – help me build a directory of activities proven by maths teachers as useful.

Unlike some other subjects where you may have the students create something to submit, playing with a widget doesn’t produce anything. So, what evidence do you have that the students are doing anything? Of course, you’re circulating around the room – but there is nowhere in my room where I can see every screen at once, mainly because the viewing angle is narrow for these netbook screens and my room is fairly small, so the last row of seats is just centimetres from the back wall. For a low motivation, low ability class, some less structured time on a widget could be fairly unproductive.

I think a couple of ways around this are:

• add a little structure with a worksheet they have to fill in (see more below)
• record some results in their work book (there’s no way we’re getting rid of exercise books in Maths)
• capture some screenshots that the teacher might check

The worksheet idea… say you were using the “Algebra Balance Scales” activity above a worksheet might look something like this:

1. Have a go at three equations of the form 3x + 2 = 8. Show the steps you used to solve one of the equations.
2. Have a go at three equations of the form 3x + 2 = x + 6. Show the steps you used to solve one of the equations.
3. Use the Create Problem button to enter this equation, 5x + 2 = 7, and then solve it.
4. Use the Create Problem button to enter this equation, 3x + 7 = 4x + 6, and then solve it.

I’ve made this into a worksheet, available below.

Algebra Balance Scales

Some ideas for widget makers:

• Support your widget with some specific, written down, activities; even something printable (shock horror!)
• If you make a widget that takes students through some steps to get to an end results, have some code words they need to collect along the way and a secret place on your web-site where teachers can find out the keywords.
• Add a simple scoring mechanism to activities to at least show attempts, even if not scoring right/wrong.

How are you using widgets like this and ensuring students are engaged?

If you like this idea and make some worksheets to support online activities, please share.