Teaching equations

Tuesday, 15 September 2009 | 5 Comments

Year 8 were recently assessed on solving equations and I was a little perplexed by the results.

For one-step equations like,

54% of students in one of my classes got both questions right. But even many of those showed a solution like this:

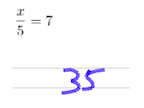
Student solution to x/5=7

rather than something a little more formal like:

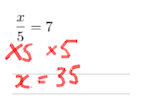
Model solution to x/5=7

I can understand, these are simple questions with obvious solutions.

Question 2 were two step equations like these:

This is where I noticed things going wrong. These questions are a little beyond intuition – 27% of the students got both correct. The wrong answers tended to show an intuitive approach or a guess and check approach using a calculator.

My conclusion from looking at this task – when it comes to assessment, many of these students reverted to prior knowledge gained in primary school rather than a more formal process they’ve seen this year.

This can be clearly seen when only 4% of students correctly solved:

I teach equations by jumping into the formal solution in the first lesson. Having said that, I “jump in” pretty gently with a fairly simple idea… keeping a seesaw balanced:

Solving Equations from Simon Job on Vimeo.

From here, I’ll start with one-step equations, and over subsequent lessons build up the complexity of the equations we’re solving.

I have looked at some of the explanatory methods like “backtracking”, but found that my students struggled with those even more. (For further discussion of three methods: 1. Guess, Check and Improve, 2. Backtracking and 3. Balancing, have a look at this PowerPoint file titled Reviewing the Models for Solving Equations found on the MANSW site.)

Dan Greene at The Exponential Curve is also discussing this issue in his post: Algebra 1: Solving Equations.

What’s my solution? I don’t really have one at the moment… have you seen the same issue of students reverting to prior knowledge, even though it’s no longer adequate? What am I doing wrong here?

Posted in • Lesson Idea • Algebra • Equations • Media • Video • Reflection | Short URL: http://mths.co/1629

Comments

Glenn on 15 September 09 at 11:04 PM #

I struggle with the same thing, but this year I taught it differently, and I had many learners say it helped. I have not given the test yet, but initial results on assignments look promising. I have a post on using SADMEP as a hook (just like the learners have PEMDAS as a hook for expressions) in solving equations. Check out my blog for details. [url=http://mrwaddell.edublogs.org/2009/09/13/hooks-and-ladders-in-alg-2/]http://mrwaddell.edublogs.org/2009/09/13/hooks-and-ladders-in-alg-2/[/url]

Ryan on 19 September 09 at 01:36 AM #

I can definitely relate to the struggles of teaching students to solve equations. I have used the balancing method more extensively with my students, because I can show them physically what is going on. In fact, I will use a balance scale to illustrate the idea. This is ok, but I thing the bottom line is that students have to be given ample opportunity to try out several methods in order to discover which one(s) work best for them. Glenn, I find the idea of SADMEP intriguing and I will definitely be trying that with my students this semester. Thank you for sharing.

Lois Lindemann on 12 October 09 at 04:31 PM #

I can relate to this, I have a Y10 group who are fairly weak mathematicians and who are struggling with exactly the same thing. They can work with a seesaw (actually my old kitchen scales) but it doesn't seem to help when we move onto symbols. We solved two step equations with machine chains (because they had an exam coming up and we needed the marks), but that doesn't help them get very far. I've left equations for now and am doing lots of little algebra skills prcatice sessions, week in, week out. Of course I don't know yet if improved algebra manipulation will help with the equations, I'll find out the answer to that in a few weeks time.

Sam Shah on 13 October 09 at 04:27 AM #

Nice post. I wonder if you show your students next year the results from this year -- before they start the unit -- if it would help. Because perhaps students aren't learning/appreciating the "method" because they can just *see* the answers for the first type of problem. But telling them that going through the step of showing their work will help them understand and work the harder type of problem encountered later. We start easy now so we can do hard later. In other words, before you go into the topic, would it help to show them the forest, so they know how important it is they stay on the path you're guiding them through? Just an idea. I found this post powerful, and wonder if your kids next year would also!

author

Simon Job on 15 October 09 at 06:41 AM #

Thanks for the interesting comments. I'm thinking that next time - which is Yr 9 in a couple of weeks - I might try starting out with basic questions and gradually increasing the difficulty. Students work at their own pace until they get stuck. Hoping to see correct answers at each level to move to the next. When they get stuck, they may see the need for a method. Obviously, the one daunting thing is the class staggering and having students at so many different levels -- although the Year 9 class have recently got netbooks, so I might be able to put some of the teaching online for those that get ahead - in essence, making it a self-paced, self-taught unit.

Get updates…

Email newsletter Subscribe to blog

Twitter Facebook Pinterest

About

Simon Job — eleventh year of teaching maths in a public high school in Western Sydney, Australia.
MathsClass is about teaching and learning in a maths classroom. more→

Elsewhere

@simonjob
updates via @mathslinks

MathsClass