Being too helpful?
Saturday, 25 August 2012 | 6 Comments
As I said in an earlier post...
2012 is looking like a year of quiet reflection (i.e. maybe not much on this blog), contemplation and trial and error.
Here is some recent thinking, please comment.
Lowering standards is not ok, but increasingly existing methods of assisting students to meet standards is not working. Therefore, the way I “teach” to help students reach the standard must adapt.
What is surprising for me is the timeframe in which the learning needs of students has changed. If I was teaching how I am today, 7 years ago when I started, I would have been brilliant. Today it is still not enough.
I think students are requiring:
- more and more structure to complete straightforward tasks.
- immediate feedback that is really not achievable without the use of technology.
- technology to aid and enhance, enabling them to learn in a different way to how we might have taught in the past.
Here’s something I did recently, and I’m still debating the validity of the approach.
The syllabus says, MS5.2.2:
using the formula V = ⅓Ah to find the volume of pyramids and cones where A is the base area and h is the perpendicular height
During class time my focus is on having the students apply this formula to solve basic problems, identifying the necessary dimensions to substitute into the formula. When it comes to a test, I would give the students the formula because they rarely are motivated to remember formulae.
We then went to Mathletics to review finding the volume of pyramids, cones, cylinders and spheres using the formulae we had previously applied. To me, Mathletics is taking an old style approach, i.e. here is a shape, what is it’s volume?
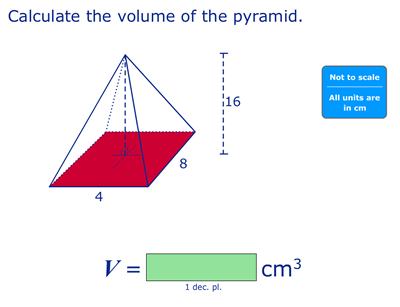
[Note: I’m not having a go at Mathletics, in fact, I think they know that the current method is not adequate. They recently had Dan Meyer out to talk to their developers.]
Anyway, leaving it at that would have been a pointless lesson. I made this available to the students.
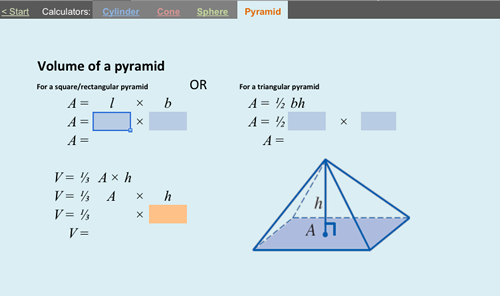
 It’s a calculator for finding the volume of these shapes where all the students have to do is input the variables. For a rectangular pyramid entering the length and breadth of the base, and the height of the pyramid is all that is required. Results were certainly better than could be expected without using the calculator.
It’s a calculator for finding the volume of these shapes where all the students have to do is input the variables. For a rectangular pyramid entering the length and breadth of the base, and the height of the pyramid is all that is required. Results were certainly better than could be expected without using the calculator.
Dan Meyer once said Be less helpful am I being too helpful? My current thought is that I’ve provided a suitable tool to help students move past the mechanics of the calculation potentially allowing them to solve more realistic problems.
Have I taken a step too far or does using a tool like this make solving problems more like the application of mathematics might look like in their future?
Download the calculator below:
Posted in • Lesson Idea • Volume • Software • Excel • Tools | Short URL: http://mths.co/2711
Post a comment
Commenting is not available in this channel entry.New Subscribe to the …
MathsLinksemail newsletter
Get updates…
About
Simon Job — eleventh year of teaching maths in a public high school in Western Sydney, Australia.
MathsClass is about teaching and learning in a maths classroom. more→
Archive
Elsewhere
 @simonjob
@simonjob
updates via  @mathslinks
@mathslinks
Recently read/found.
Being a Vector is not Mutually Exclusive – Ringo Mok
maths vectorsInstagram
Gcf howie_hua maths
Comments
author