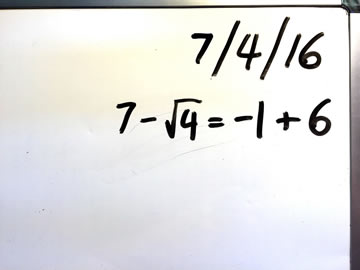A look at the new Mathematics 7-10 syllabus for NSW
Saturday, 11 February 2023 | 0 Comments
This post is a single point to access some of the resources I'm developing as I investigate the new Mathematics K-10 Syllabus (2022) released by the NSW Education Standards Authority.
Documents below are based on Mathematics K-10 Syllabus, NESA, 2022. They are not authorised NESA documents. They are for planning and review purposes only. Shared for use by teachers in schools only.
Over on MathsLinks, I've started aligning content to the new K-10 syllabus.
1. Continuum of learning
To help understand the Core/Path designation and the connections to Stage 6 courses.
2. Comparing old and new outcomes
Working with my faculty, we're going to compare the old syllabus outcomes with the new. Here are some A5 cards with the Stage 4/5 outcomes from both, for the activity I'll print them on different colour paper.
Dates as Operations 2018
Saturday, 03 February 2018 | 0 Comments
In 2017 I published a post Dates as operations 2017 - a collaborative effort to write a mathematical statement from the digits of the date.
Here is the 2018 version. To quickly access in class type gomaths.net/dates into your address bar.
Updated for 2019: gomaths.net/dates
Updated for 2021: gomaths.net/dates
Updated for 2022: gomaths.net/dates
Updated for 2023: gomaths.net/dates
A look at the new Mathematics Standard syllabus for NSW
Monday, 03 April 2017 | 0 Comments
Updated: 23/06/2017
 DoE Numeracy Conference: the presentation is item 5a below. The continuum handout is item 6. NOTE, I have added an amendment after the presentation upon reading the NESA Course Descriptions released 21/6/17. The continuum handout is correct as per the Syllabus but incorrect as per the Course Descriptions.
DoE Numeracy Conference: the presentation is item 5a below. The continuum handout is item 6. NOTE, I have added an amendment after the presentation upon reading the NESA Course Descriptions released 21/6/17. The continuum handout is correct as per the Syllabus but incorrect as per the Course Descriptions.
This post is a single point to access some of the resources I'm developing as I investigate the new Mathematics Standard Stage 6 Syllabus (2017) released by the NSW Education Standards Authority.
1. Course Description: a summary view of the new syllabus
^Updated for November 2017
2. Standard syllabus versus General syllabus: includes each item in the new syllabus mapped to the old syllabus. Also includes links to the Australian Curriculum. This is not official, rather my best guess.
3. Standard syllabus versus General syllabus - Presentation: an overview of the topics in the new syllabus mapped to the old syllabus. Slides designed for presentation.
4. Standard syllabus mapped to General syllabus: an overview of the topics in the new syllabus mapped to the old syllabus. An abbreviated version of #2 above and slightly more detail than #3.
5. 23/04/2017 Presentation: Mathematics Standard - What's new, what stays the same?: a slide package that I will be presenting at Staff Development Day to my faculty. For that reason, some of the slides may be unclear without the context I will provide.
5a. 22/6/2017 Presentation: Mathematics Standard - Orange is the new standard: a slide package presented at Department of Education Numeracy for Learning K-12 Conference
23/6/2017 NESA Course Descriptions: they were released the day before I presented, but I had not read them. There are items in the course descriptions that are different to the syllabus and clarify other points. See this amendment.
6. 29/04/2017 Mathematics Continuum of Learning: from the Mathematics 7-10 Syllabus Continuum of Learning, I have used the new Stage 6 Standard syllabus to attempt to extend the Continuum of Learning. 24/6/17: Updated to include the assumed knowledge as identified in the Course Descriptions.
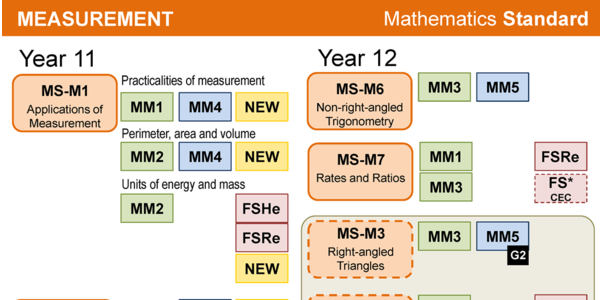
The interest points for me: Ratios and Rates: 5.2 Ratio and Rates not listed as required and no Rates and Ratios in Year 11. Measurement makes this almighty appearance in Year 11 and then turns into Trig and scale drawing. Mass makes a reappearance after last appearing in Stage 3.
Documents above based on Mathematics Standard Stage Syllabus, NESA, 2017. They are not authorised NESA documents. They are for planning and review purposes only. Shared for use by teachers in schools only.
Over on MathsLinks, I've started aligning content to the new Standard syllabus.
Dates as Operations 2017
Wednesday, 28 December 2016 | 0 Comments
Like most teachers I write the date at the top of the whiteboard each day. As an extra point of interest, in 2016 I endeavoured to write a number sentence using the digits of the date, in order, underneath the date.
For example:
7/4/16 7 - √4 = -1 + 6
27/5/16 2 + 7 - 5 = √16
(Date written as dd/mm/yy)
I didn't specifically refer to the sentence, nor make it an activity in class. A senior student in one class made a point of completing the number sentence if I hadn't. Another student in my roll class regularly pointed out if I had not written a sentence for the day.
In 2016 I had some help completing a list of sentences.
If you'd like to contribute to a list for 2017 (or just use the list) visit this Google Sheet:
For 2017, I have columns for two formats of the date dd/mm/yy and dd/mm/yyyy.
Data values vs scores
Sunday, 30 October 2016 | 0 Comments
Note for self really,
In the new NSW Syllabus for Mathematics K-10 what used to be referred to as scores when analysing data are now called data values.
So the definition of mean is written as
$$\bar{x}=\frac{\text{sum of data values}}{\text{number of data values}}$$
Continue to all entries from October 2016
See the Archives for more…
New Subscribe to the …
MathsLinksemail newsletter
Get updates…
About
Simon Job — eleventh year of teaching maths in a public high school in Western Sydney, Australia.
MathsClass is about teaching and learning in a maths classroom. more→
Archive
Elsewhere
 @simonjob
@simonjob
updates via  @mathslinks
@mathslinks
Recently read/found.
Instagram
Gcf howie_hua maths37 Heaven
maths interestingEddie Woo’s expert maths team cut back under education department restructure
teaching mathsConcrete example that shows why 2^0 = 1.
maths indexnotationSydney University abandons HSC prerequisites in diversity push
maths